「静圧」は流水圧と静水圧
流体力学では圧力という言葉は大概は静圧のことを指します。ベルヌーイの定理を勉強してると、動圧、全圧、ゲージ圧、…とやたらと「~圧」という言葉出てきますが、圧力は静圧だとまず思ってくだしさい。同時に、ナビエ-ストークス方程式の圧力項\(\partial p/\partial x\)は、静圧を扱っていることを再認識していただければと思います。
さて、静圧についてもう一歩踏み込んでいきましょう。静圧は流水圧と静水圧というもに分解することができます。なので、\(静圧p=流水圧p_{\scriptsize{\rm{R}}}+静水圧p_{\scriptsize{\rm{S}}}\)と書けます。流水圧は、圧力勾配\(\partial p/\partial x\)によって引き起こされる圧力で、静水圧は重力などの外力に抗しようと発生する圧力です。以前、圧力は分子の熱運動と説明しましたが、流水圧も静水圧も、いずれも分子振動から発生する圧力です。
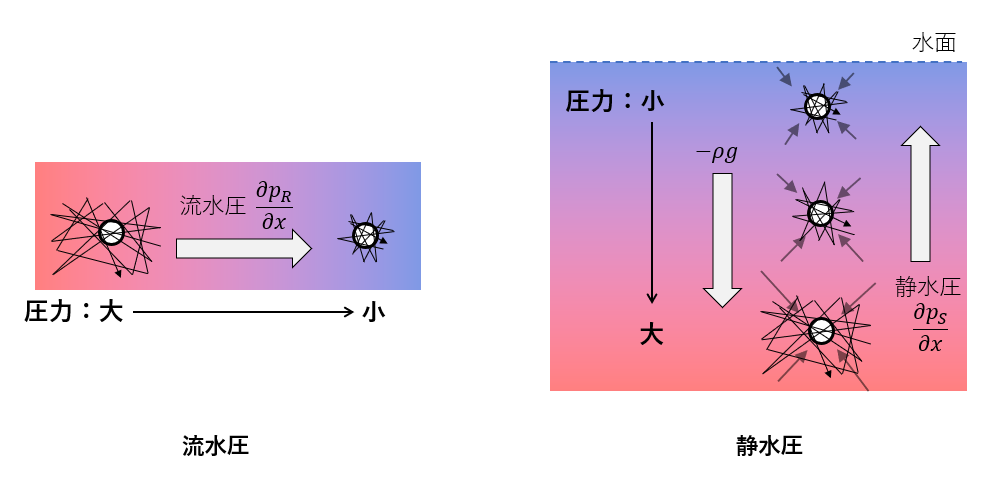
重力の影響を考える必要のないときは
\begin{eqnarray} \cfrac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}=-\cfrac{1}{\rho}\nabla p +\nu \Delta\boldsymbol{u} \tag{1}\end{eqnarray}
の定番の数式型でよいのですが、動圧と位置エネルギーを考慮した力学的エネルギーの関係を物理的に正しく把握するには、重力と静水圧の力のつり合い
\begin{eqnarray} 0 = \nabla p_{\scriptsize{\rm{S}}} + \rho g \end{eqnarray}
を式(1)に加えた
\begin{eqnarray} \cfrac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}=-\cfrac{1}{\rho}\nabla (p_{\scriptsize{\rm{R}}}+p_{\scriptsize{\rm{S}}}) +\nu \Delta\boldsymbol{u}-g \tag{2}\end{eqnarray}
をもとに、考え直す必要があります。
圧力計測は静圧を対象としており、静水圧、流水圧、動圧、全圧等を直接測定することは基本的にできません。静水圧と流水圧は静圧から切り分けることはできませんので、静水圧か流水圧を0にして静圧から読み取る方法等があります。動圧については、流速を測定して\(\rho\, u^2/2\)に換算するか、ピトー管のように動圧を静圧に変換して読み取る方法があります。
圧力の意味はエネルギーなのだ‼
さて、超有名式「ベルヌーイの定理」
\begin{eqnarray} p+\cfrac{1}{2}\rho\, u^2+\rho gh= \rm{const} \end{eqnarray}
は、速度や圧力を概算する公式ツールとして使って終わってしまう人が多いかと思います。ベルヌーイの定理はエネルギーの保存則だと教え込まれますが、なぜ圧力とエネルギーが同等に扱えるのか説明される機会が少ないので解説していきます。
僕らは高校で運動方程式
\begin{eqnarray} m\boldsymbol{a}=\boldsymbol{F} \end{eqnarray}
を習いました。流体力学ではナビエ-ストークス方程式(1)または(2)が、運動方程式に該当します。左辺が加速度であることから、運動方程式と読み取れるかと思います。ちなみに流体力学で、質量を質量密度\(\rho\)で考えますから
\begin{eqnarray} \rho\cfrac{d \boldsymbol{u}}{d t}=-\nabla (p_{\scriptsize{\rm{R}}}+p_{\scriptsize{\rm{S}}}) +\rho\nu \Delta\boldsymbol{u}-\rho g \qquad ※説明上ラグランジュ形にしてます\end{eqnarray}
と書いた方が、運動方程式と見立てやすいかもしれません。
そして、高校の物理では力を位置で積分した
\begin{eqnarray} \int_x(m\boldsymbol{a})dx=\int_x \boldsymbol{F}dx\end{eqnarray}
がエネルギーになると習いました。これに倣い式(2)を積分すると
\begin{eqnarray} \rho\cfrac{\partial \boldsymbol{u}}{\partial t}+\rho(\boldsymbol{u}\cdot\nabla)\boldsymbol{u} &=& -\nabla (p_{\scriptsize{R}}+p_{\scriptsize{S}}) +\rho\nu \Delta\boldsymbol{u}-\rho g \\ \downarrow積分\hspace{0.5em}&\quad&\hspace{3em}\downarrow積分\hspace{5em}\downarrow 積分\\ \rho\frac{1}{2}u^2 \quad &=& \quad -(p_{\scriptsize{R}}+p_{\scriptsize{S}}) \hspace{3.5em} -\rho gh \quad +\rm{const} .\end{eqnarray}
\(\rm{const} \)は全エネルギーのことで全圧と呼ばれるものです。ベルヌーイの定理は、非圧縮、摩擦、渦無し等の条件で縛って、積分をするにしてももう少し複雑な過程を経て算出されますが、まずは、「運動方程式と力学的エネルギー」の関係が「ナビエ-ストークス方程式とベルヌーイの定理」の関係にあることを掴んでいただければと思います。
単位についても、流体力学は単位体積を基準に考えることから、エネルギーに単位体積を取ると\(\rm{[N\cdot m]/ [m^3]=[Pa]}\)となり、圧力がエネルギーとして考えられることが分かります。
「動圧」と流水圧
動圧\(\rho u^2/2\)は運動エネルギーであって、それ以上の深い意味はありません。エネルギーは保存則が成り立ち物理的に取扱いやすい量なので、その一貫で動圧が定義されているだけです。
動圧と静圧の関係を考えるとき、翼の先端に淀み点が発生し圧力が高くなる問題が、しばしば引き合いに出されます。流速を持った流体が淀み点に近づき、動圧が静圧に変換されているとされていますが、運動エネルギーを持ったが流体粒子が淀み点で行き場を失い、運動エネルギーを静圧に、つまり分子の運動エネルギーになり、圧力となって表れているのです。
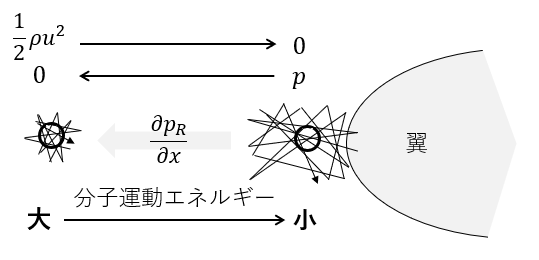
また、この問題は重力を考慮しないことが前提となっていて、\(p=p_{\scriptsize{\rm{R}}}\)であることが分かります。つまり、動圧とは流水圧がトレードオフの関係になっていることが分かります。
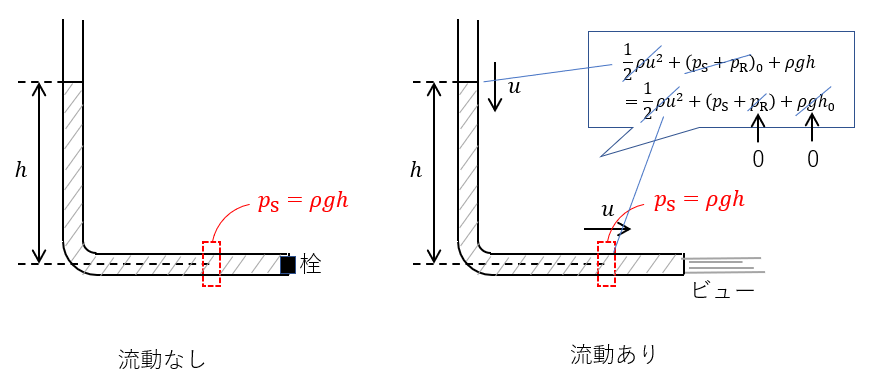
「静水圧」と位置エネルギー
位置エネルギーは静水圧とつり合いの関係にあるもので、そのことに尽きます。流動があろうとなかろうと、流体内部では、位置エネルギーや静水圧は変動することがありません。
ベルヌーイの定理のまとめ
以上、エネルギー保存則
\begin{eqnarray} \cfrac{1}{2}\rho u^2+(p_{\scriptsize{\rm{R}}}+p_{\scriptsize{\rm{S}}}) +\rho gh = \rm{const}_0 \end{eqnarray}
は同時に、「流水圧は動圧との保存則」と、「静水圧は位置エネルギーとの保存」である
\begin{eqnarray} \cfrac{1}{2}\rho u^2+p_{\scriptsize{\rm{R}}} = \rm{const}_1, \\ p_{\scriptsize{\rm{S}}} +\rho gh = \rm{const}_2, \end{eqnarray}
が成立します。特に\(p_{\scriptsize{\rm{S}}}\)と\(\rho gh\)は、流動があろうとなかろうと空間的に変動しないものなので基本的に考慮する必要のない量です。
考慮すべき場面は流体が外部条件で圧力が決まったり、流体質量で変動が発生する特殊な場面に限ります。
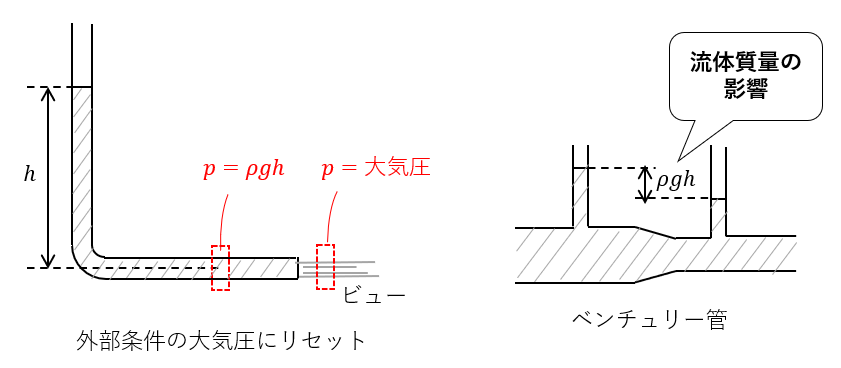
そして最後に、「~圧」の総集結図を作ってみました。こんな感じでしょうか。
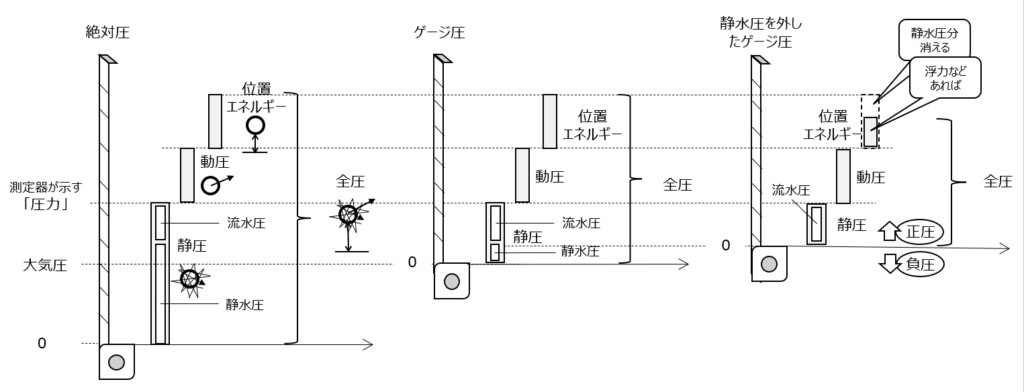
実用上の圧力表示
そのため、流体で満たされた閉じた空間では式(1)の静水圧は無視したナビエ-ストークス方程式を使います。静水圧を無視することで、圧力分布図から圧力勾配による力の発生をダイレクトに読み取れる利点があります。
有限体積法の流体解析ソフトFLUENTは、圧力分布のデフォルト設定が流水圧で表示されるようになっています。静圧を確認するときは「静水圧を加味した静圧」というものが用意されています。
一方、粒子法の流体解析ソフトParticleworksは、開いた系を扱うことが多いため、静水圧を加味した状態で圧力表示されます。
開いた系のベルヌーイの定理 (追記2023/03/21)
開いた系のエンタルピーについて
\begin{align}
h=u_1 + p + \cfrac{1}{2}\rho v^2
\end{align}
という式が出てきます.また,エネルギーは保存則下で\(h=\rm{const}\)とし,圧力も一定であるとすると,\(u_1\)と\(\frac{1}{2}\rho v^2\)は交換関係になることが分かります.
\begin{align}
u_1 + \cfrac{1}{2}\rho v^2 = u_2
\end{align}
と変換後の内部エネルギー\(u_2\)とした場合,対流として存在していた\(v\)は,熱になって分子運動\(\bar{v}\)に変わったことを意味し,つまり摩擦で対流が消失したことになります.内部エネルギーを速度とみなせることは,記事”温度とは何か“に記載してます.


コメント