ナビエ-ストークス方程式の圧力項を導出するとき、圧力が物体にかかる力を考慮してガウスの発散定理を使って、解説していくれる先生は沢山います。うん、この解説はとっても大事です。大事ですが、
\begin{eqnarray}\cfrac{\partial u_i}{\partial t}+u_j\cfrac{\partial u_i}{\partial x_j}=-\cfrac{1}{\rho}\cfrac{\partial p}{\partial x_i}+\nu\cfrac{\partial^2 u_i}{\partial {x_j}\partial {x_j}} \qquad i=1,2,3 \tag{1}\end{eqnarray}
と書くと、\(u_i\)と\(p\)が並んでいるのがどこかモヤモヤします。だって、質量\(\rho\)も渦度\(\omega_i\)も温度\(T\)も
\begin{eqnarray} 質量保存則:&&\cfrac{\partial \rho}{\partial t}+\cfrac{\partial (\rho u_j)}{\partial x_j}=0, \\ 渦度方程式:&& \cfrac{\partial \omega_i}{\partial t} + u_j\cfrac{\partial \omega_i}{\partial x_j}=\omega_j\cfrac{\partial u_i}{\partial x_j} + \nu\cfrac{\partial^2 \omega_i}{\partial {x_j}\partial {x_j}},\qquad i=1,2,3 \\ 温度の輸送方程式:&& \cfrac{\partial T}{\partial t}+u_j\cfrac{\partial T}{\partial x_j}=\kappa\cfrac{\partial^2 T}{\partial {x_j}\partial {x_j}} \end{eqnarray}
と、それぞれの式のそれぞれの項に\(\rho,\omega_i,T\)が入り「\(\rho,\omega_i,T\)の方程式なんだなぁ」「\(\rho,\omega_i,T\)は解けそうだなぁ」と分かります。しかし、式(1)についてはポッ!と\(p\)が入る…
実は、流体粒子を分子レベルで考えてみると、圧力も分子の速度(運動量)を意味していまして、ナビエ-ストークス方程式に圧力が入っていることに合理的説明をすることができるのです。
圧力は分子運動
圧力は熱的な分子運動であって、物体にかかる圧力は飛び回っている分子が無数にぶつかることで形成されます。また、物体を介さなくても同じように、粒子同士がぶつかり合って空間上に圧力場が形成されます。

さて、圧力勾配のある流れ場で、大きな速度を持った流体粒子が圧力の低い所から高い所に向かうとき、流速が段々落ちていって、終いには止まってしまいますよね。これは、流体が持つ速度が分子運動に変換されるために起こっているのです。非圧縮流体と扱っているのに関わらず、計測では捉えきれないほどの微量な圧縮であったり温度変化などが起きて、圧力として捉えられ大きさになって現れるのです。

今井功著「流体力学(前編)」には数式を交えて解説されていて、なかなかここまで説明してくれる人は希だったので、初めて読んだときとは感動しました。
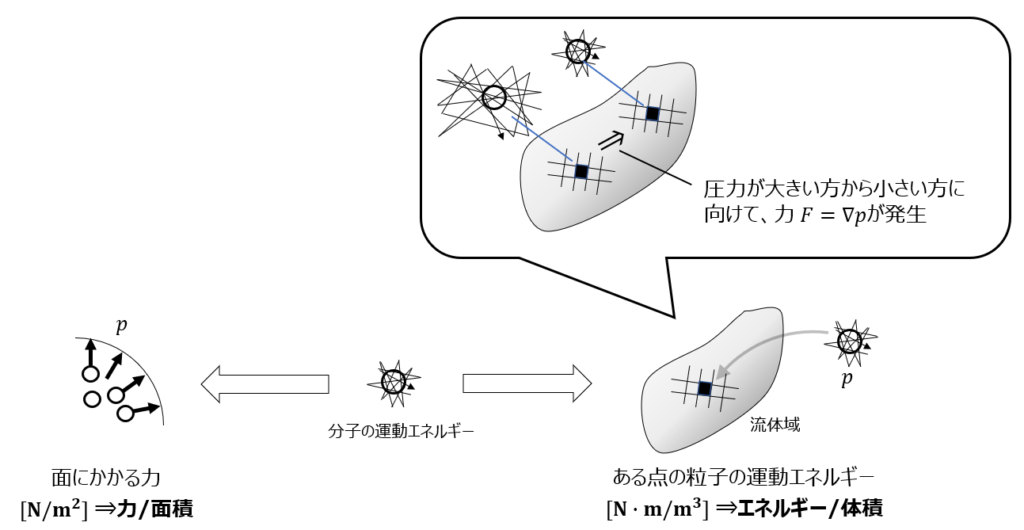
それと圧力はエネルギーであることも押さえておきましょう。単位体積を取ると\(\rm{[N\cdot m]/ [m^3]=[Pa]}\)となり、圧力がエネルギーとして考えられることが分かります。圧力は面にかかる力であるのはご存知だと思いますが、下図のようにある点で見た時は、流体粒子が持つエネルギーだとも解釈できます。圧力は重力のように、ポテンシャルの役割を持つエネルギーであります。
分らなかった人に向けて
今回の話は、流体の圧力項のイメージが出来上がっている人を向けて書きました。さっぱり分らなかった人は、圧力がどう流動に影響を与えるのか想像するのに慣れていないのが原因だと思います。なので、まずは圧力場の見方に慣れてみてください。
そのためには「流体は圧力勾配\(\partial p/\partial x\)によって加速される!」というフレーズをとりあえず丸暗記し、流体の運動を考えないといけない場面があったら、このフレーズを唱えながら、
(1) 圧力が設定された問題かチェック
(2)圧力勾配の高低方向を確認
(3)圧力勾配の高い方から低い方に加速記号の矢印を図示
を丁寧に実施してみてください。段々と圧力の扱いに慣れると思います。慣れてきたら、分子運動を想像しながら実施すると圧力と流体運動のイメージ力が磨かれると思いますよ。


コメント