拡散

　空間上に起伏や凹凸状を持って分布するある物理量が，時間経過と伴に滑らかになっていく現象を拡散と呼びます．波立つ水槽の水が時間経過し収まっていったり，温度ムラのある室内空間が次第に均一化していったりする現象です．

　拡散現象は正確には保存量の場合に成立し，保存量を\(\phi\)とすると
\begin{align}
\cfrac{\partial \phi(x,t)}{\partial t}=k \Delta \phi ,
\end{align}
拡張した書き方だと
\begin{align}
\cfrac{\partial \phi}{\partial t}=\nabla\cdot (k \nabla \phi) ,
\end{align}
とかになります．それではまず，温度に当てはめた場合の式と現象をもう少し覗いてみましょう．

　保存量の代表例で熱エネルギーを考えてみましょう．空間上に熱量\(Q\,\rm[J/m^3]\)を持った状態で存在していると
\begin{align}
\cfrac{\partial Q(t,x)}{\partial t}
=\cfrac{\partial }{\partial x}\biggl( \kappa\cfrac{\partial Q}{\partial x} \biggr),
\tag{1}\label{eq:heat-diff-eq}
\end{align}
となります．
　直感的に分かりやすいように，ここで，温度ムラの話に繋げていきましょう．
\begin{align}
Q(t,x)=\rho c_p(T(x,t)-T_0)\tag{2}\label{eq:specific-heat}
\end{align}
とおいてみると，式(\ref{eq:heat-diff-eq})(\ref{eq:specific-heat})より
\begin{align}
\rho c_p\cfrac{\partial (T(x,t)-T_0)}{\partial t}
=\rho c_p\cfrac{\partial }{\partial x}
\biggl( \kappa\cfrac{\partial (T-T_0)}{\partial x} \biggr),
\end{align}
すなわち
\begin{align}
\cfrac{\partial T(x,t)}{\partial t}
=\cfrac{\partial }{\partial x}
\biggl( \kappa\cfrac{\partial T}{\partial x} \biggr),
\tag{3}\label{eq:temp-diff-eq}
\end{align}
と，式(\ref{eq:specific-heat})をおくことで，温度分布が平滑化される式が表現されます．温度は分子の運動を示すものであって，高温群と低温群が同一空間にあれば分子の運動によって分布は均一になりますし(乱流拡散)，分子同士の衝突による運動量のやり取り(粘性拡散)も同時に進みます．これらの要因で温度の平滑化がされるようになっています．

　次は運動量の拡散についてです．粘度の測定実験モデルを使ってまず，流体中に発生するせん断応力を捉えられるようにしましょう．右図のように平面と僅かな間隔を空けて上面に回転平板を設置し，その隙間に流体があるとします．回転平板には応力\(\tau\)をかけます．隙間を僅かにすることで速度の勾配は直線的になり
\begin{align}
\tau(t)
=\mu\biggl(\cfrac{\delta u(t)}{\delta y}\biggr)
\tag{4}\label{eq:share-stress}
\end{align}
と，速度勾配\((\delta u/\delta y)\)と\(\tau\)は定数\(\mu\)を挟んだ比例関係にあります．実験ではせん断応力を与えて速度勾配を作る手順となりますが，実際はこの逆も成り立ちます．つまり，速度勾配が大きく発達するほどせん断応力は大きくなります．
　そして，このせん断応力と速度分布は流体中にも存在します．説明手順は次の通りです．流体中で引き起こされるせん断応力は，回転平面の仕事で発生するせん断応力に引きずられ，流速と同方向の力となります．もし，固体が底面にあった場合は反力が発生しますが，流体の場合は異なる振舞いをします．

次に，実験モデルの固体平面を流体への置き換えについてです．思考実験的ですが，下図の順番で考えていくと成り立つことが感覚的に分かると思います．下面に弱い回転を与え，固体を測定対象流体に置き換えるといったものです．

ここまでは狭い隙間に挟まれた流体に焦点を当ててきましたが，更に下図の様に流体を挟んでいる流体がまた流体に挟まれたものと考えれば，せん断応力は連続的に存在していることにも気付きます．このような思考手順で，流体中の速度分布とせん断応力分布のあり方を掴むことができます．

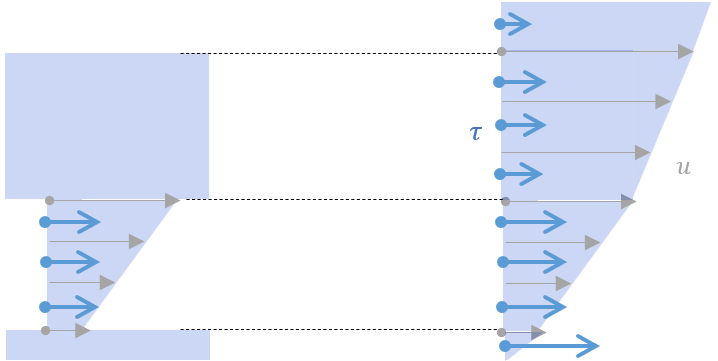
　以上，式(\(\ref{eq:share-stress}\))が流体中でも成り立つことを説明してきました．次に，\(\delta \rightarrow 0\)とし \(\mu=\rho\nu\)としましょう．\(\rho\)は密度です．なぜ密度を導入したかというと，式(\(\ref{eq:share-stress}\))は
\begin{align}
\tau_x(y,t)
=\nu\cfrac{\partial ( \rho u(y,t))}{\partial y}
\tag{5}\label{eq:share-stress-2}
\end{align}
となり運動量の方程式に書き換えることができ，本ブログの主人公である保存量の「運動量」によってせん断応力が引き起こされるのに気付きます．流体粒子は分子運動論的に考えて衝突運動を繰り返し，運動量の交換を繰り返し行います．そのため，運動量の大きい側が小さい側に移っていく現象が起きます．また，流体は乱流状態にあるとき無数の渦の集合体と考えることができ，渦によって運動量が大きい側から小さい側に運ばれることも起きます．

　ここまで話が小難しかったですが，「まぁ，何はともあれ，せん断応力の式があるので\(F=ma\)だからこの力によって流体は加速減速されるのだなぁ」と結論付けたくなるでしょう．いやいや，一呼吸置いてください．圧力は流体中ではポテンシャルエネルギーとして扱われ，勾配によって加速される説明を以前しました．そう，応力については勾配によって加速します．なので，
\begin{align}
\cfrac{\partial ( \rho u)}{\partial t}
=\cfrac{\partial \, \tau_{xy}}{\partial y}
\tag{6}\label{eq:viscosity-term-1comp}
\end{align}
の式が成立します．また，この延長で考えて，せん断という言葉が似合わなくなりますが，せん断応力方向の勾配によっても加速が生じます．

　そして，上図のように3成分あるので，
\begin{align}
\cfrac{\partial ( \rho u)}{\partial t}
&=\cfrac{\partial \, \tau_{xx}}{\partial x}
+\cfrac{\partial \, \tau_{xy}}{\partial y}
+\cfrac{\partial \, \tau_{xz}}{\partial z} \\
&=\cfrac{\partial}{\partial x}\biggl(\nu\cfrac{\partial ( \rho u)}{\partial x}\biggr)
+\cfrac{\partial }{\partial y}\biggl(\nu\cfrac{\partial ( \rho u)}{\partial y}\biggr)
+\cfrac{\partial}{\partial z}\biggl(\nu\cfrac{\partial ( \rho u)}{\partial z}\biggr)
\tag{7}\label{eq:viscosity-term-3comp}
\end{align}
となります．運動量を3成分に拡張すると
\begin{align}
\cfrac{\partial ( \rho \boldsymbol{u})}{\partial t}
=\nabla\cdot(\nu\nabla(\rho\boldsymbol{u})),
\tag{8}\label{eq:viscosity-term-9comp}
\end{align}
ただ，ベクトル表記では誤認しやすいので
\begin{align}
\cfrac{\partial ( \rho\, u_i)}{\partial t}
=\nabla\cdot(\nu\nabla(\rho\, u_i)),\qquad i=1,2,3
\tag{9}\label{eq:viscosity-term-9comp-ver2}
\end{align}
とした書き方に変えたりもできます．