導出：開いた系→閉じた系

　学生の時の話，私が気象学や流体力学をやっていると，熱の方程式がさらりと現れることがしばしばありましたが，閉じた系しか習っていないために式の扱いに確信が掴めずにいました．いや，閉じた系すらどこか掴めずにいました．周りは涼しい顔をして分かっていたようでしたが，私と同じ気持ちで過ごしている人もきっといるでしょう．
　本ブログでは既に開いた系については解説しています．今回，開いた系と閉じた系の結びつきを理解するために，気体の状態方程式と熱力学第一法則を，開いた状態から閉じた系に落としていきました．実際に導出してみると，エンタルピー，示量性と示強性，独立変数，常微分と偏微分，ガウス積分，伝熱工学等，色々な知識が試されました．ただ，それらを超えることで閉じた系が明快に理解できるはずです．

　熱力学は物理学の一分野に関わらず，機械工学に合わせて作られています．どことなく取っ付きにくいのはそのためです．近年の第三次産業革命こそITやAIに関するものですが，それ以前の第一次産業革命の「蒸気機関」や第二次産業革命の「電気・石油」などは熱とエネルギーに関すものでした．巨額な資本が動くものには自然科学も足並みを揃えざるえないのでしょう．
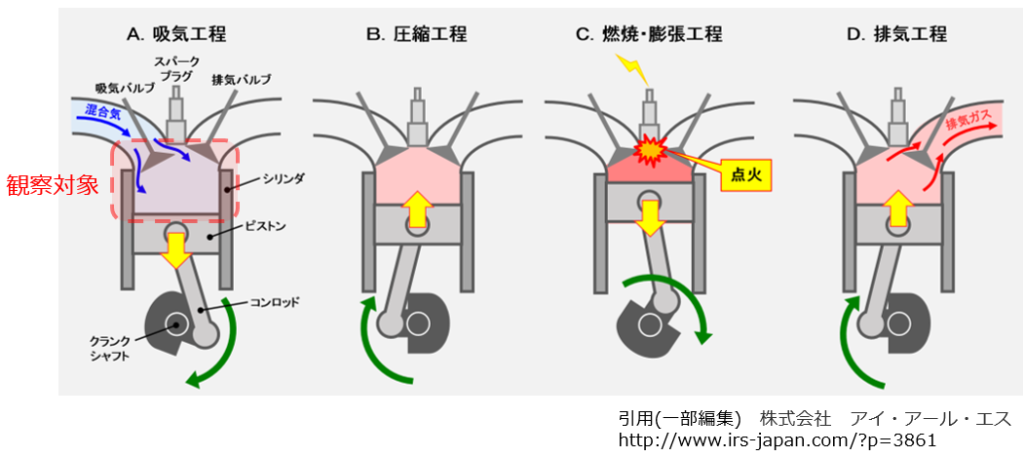
　エネルギーを取り出す機構には主にエンジン(気筒)とタービンの2系統あって，熱力学では前者をモデルにしています．どのように動いているかは下図を追ってみてください．開いた系になる瞬間や爆発があったりはしますが，シリンダ内でピストンが上下運動し閉じた状態で考えることで，考察しやすくなることは察知がつくかと思います．

　熱力学では以下(a)(b)(c)の3条件が前提で話が進められます．可逆性については本記事では触れていません．
(a)閉じた系
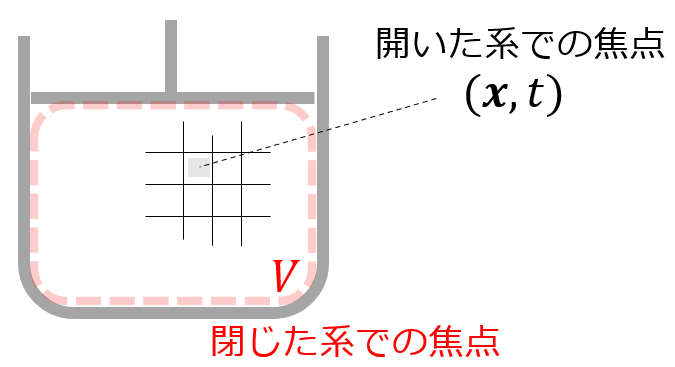
　系が密封されて系外と物質の出入りが全くないというものです．つまり系では質量保存則が成立し，系の質量を\(m\)，密度を\(\rho\)，体積を\(V\)とすると
\begin{align}
m = \int_{V(t)}\rho(\boldsymbol{x},t)dV(t) ,\tag{1}\label{eq:m_int}
\end{align}
　後に説明する条件(c)準静的の空間的一様の下では
\begin{align}
m = \rho(t) V(t) \tag{2} \label{eq:m}
\end{align}
となります．また，物質の移動がないのに関わらず熱エネルギーは系の内外を移動する点も一つのポイントとなっています．缶コーヒーは開けていなくても，温めたり冷ましたりすることできることを表しています．
(b)理想気体
　熱力学では圧縮性に富み振舞いも単純である気体をモデルにしています．状態方程式が成り立つことが前提であり，開いた系では時間\(t\)と空間\(\boldsymbol{x}\)を独立変数とした場合
\begin{align}
p(\rho(\boldsymbol{x},t),T(\boldsymbol{x},t)) = \rho R T \tag{3}\label{eq:pRTxt}
\end{align}
となります。
(c)準静的
　準静的な変化とは，系内の気体の状態を極めてゆっくり変化させていくことらしいです．本来，気筒内では温度や圧力等の物理量のムラが発生しますが，準静的に変化させると空間的に一様になります．同時に時々刻々の変化の考える必要がなくなり，変化の前後だけ考察すればよくなります．

　閉じた系の気体状態方程式の導出にあたり，まず，開いた系の気体の状態方程式(\ref{eq:pRTxt})を気筒内全体で空間積分すると
\begin{align}
\int_{V(t)}p(\boldsymbol{x},t) dV(t)
= \int_{V(t)}\rho(\boldsymbol{x},t) R T(\boldsymbol{x},t) dV(t) \tag{4}\label{eq:pRTint}
\end{align}
となりますが，(c)準静的条件の空間一様の性質により
\begin{align}
p(t)\int_{V(t)}dV(t) = \rho(t) R T(t) \int_{V(t)}dV(t)
\end{align}
\begin{align}
p(t)V(t) = \rho(t) V(t) R T(t),
\end{align}
となり，(a)閉じた系の質量保存性により
\begin{align}
p(t)V(t)= m R T(t) \tag{5}\label{eq:pRTt}
\end{align}
と閉じた系の式が完成します．式(\ref{eq:pRTxt})の単位は\({\rm [J/m^3]}\)となっているのに対し，式(\ref{eq:pRTt})では\({\rm [J]}\)と系全体の体積のエネルギー示していることにも注目してほしいです．

　開いた系で扱いやすい比エンタルピーを，ある時刻\(t\)と位置\(\boldsymbol{x}\)で
\begin{align}
h(\boldsymbol{x},t) = p(\boldsymbol{x},t) + u(\boldsymbol{x},t)
+\cfrac{1}{2}\rho\boldsymbol{v}^2(\boldsymbol{x},t)
+\rho g\boldsymbol{x}
\end{align}
とおいてみます．\(u\)は比内部エネルギーで，\(\rho\boldsymbol{v}^2/2\)は運動エネルギーです．ただし，(c)準静的条件より対流運動は起こらないので
\begin{align}
h(\boldsymbol{x},t) = p(\boldsymbol{x},t) + u(\boldsymbol{x},t) \tag{6}\label{eq:h}
\end{align}
で考え直すことになります．気筒内を空間積分して，その時間変化をとり
\begin{align}
\cfrac{\partial}{\partial t}\int_{V(t)} h(\boldsymbol{x},t) dV(t)
= \cfrac{\partial}{\partial t}\int_{V(t)} p(\boldsymbol{x},t) dV(t)
+ \cfrac{\partial}{\partial t}\int_{V(t)} u(\boldsymbol{x},t) dV(t)
\end{align}
が導出されますが，空間一様を考慮して
\begin{align}
\cfrac{d}{d t} \bigl(h(t)\, V(t)\bigr)
= \cfrac{d}{d t} \bigl(p(t)\, V(t)\bigr) + \cfrac{d}{d t} \bigl(u(t)\, V(t)\bigr), \tag{7}\label{eq:dh}
\end{align}
となります．時間のみの一変数になるため常微分に書き換えています．比エンタルピーと比内部エネルギーは示量変数なので，エンタルピーと内部エネルギーは
\begin{align}
H(t)=h(t)\, V(t), \tag{8}\label{eq:HH}\\
U(t)=u(t)\, V(t), \tag{9}\label{eq:U}
\end{align}
と書けます．式(\ref{eq:dh})に式(\ref{eq:HH})と式(\ref{eq:U})を代入して
\begin{align}
\cfrac{dH(t)}{d t}
= \biggl( V(t) \cfrac{d p(t)}{d t}+ p(t) \cfrac{d V(t)}{d t} \biggr)
+ \cfrac{dU(t)}{d t}, \tag{10}\label{eq:dHH}
\end{align}
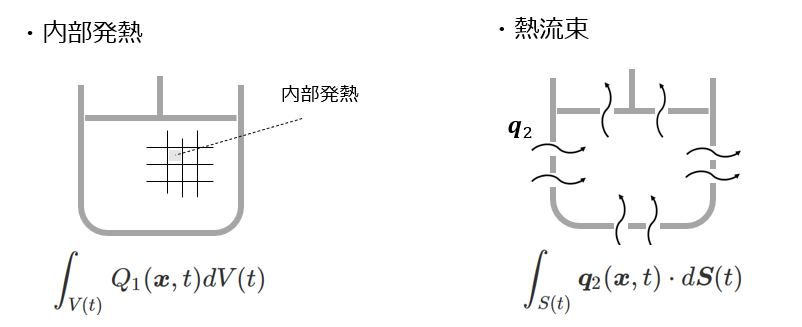
一方で，エンタルピーは内部発熱\(Q_1\)と熱流束\(\boldsymbol{q}_2\)による熱流入により温度上昇すると仮定すると
\begin{align}
\cfrac{\partial}{\partial t} &\int_{V(t)} h(\boldsymbol{x},t) dV(t) \\
&= \int_{V(t)} Q_1(\boldsymbol{x},t) dV(t)
+ \int_{S(t)}\boldsymbol{q}_2(\boldsymbol{x},t) \cdot d\boldsymbol{S}(t)
+ V(t) \cfrac{\partial p(t)}{\partial t} \tag{11}\label{eq:dQ}
\end{align}
と書けます．皆さんは\(\Delta Q=mc\Delta T\)の方が馴染みがあると思います．式(\ref{eq:dQ})はこれだと思ってください．

また，式(\ref{eq:dQ})の熱流入によるエンタルピーの上昇では圧力ポテンシャルの上昇が考慮されていないので加える必要があります．圧力ポテンシャルについては，記事”エンタルピーを復習“に記載したつもりでしたが，ちょっと説明不足かも…．今後，詳しく説明できればと思っています．
　さて，式(\ref{eq:dQ})を閉じた系に向けて簡略化していきましょう．\(Q_1\)を想定した熱力学の問題は少ないので除外し，\(\boldsymbol{q}_2\)についても
\begin{align}
\cfrac{\partial Q_2(t)}{\partial t}
= \int_{S(t)}\boldsymbol{q}_2(\boldsymbol{x},t) \cdot d\boldsymbol{S}(t)
\end{align}
と置き換えて(記事’熱伝導方程式‘)，式(\ref{eq:dQ})は
\begin{align}
\cfrac{d H(t)}{d t}
= \cfrac{d Q_2(t)}{d t}+V(t)\cfrac{d p(t)}{d t} \tag{12}\label{eq:dQ2}
\end{align}
と簡略化でき，式(\ref{eq:dHH})と式(\ref{eq:dQ2})より
\begin{align}
\cfrac{d Q_2(V(t),U(t))}{d t}
= p(t)\cfrac{d V(t)}{d t}+\cfrac{d U(t)}{d t} \tag{13}\label{eq:dQ2_t},
\end{align}
(c)準静的の変化前後だけ考えればよいことから，時間の変数を省いて
\begin{align}
d Q_2(V,U) = pdV+d U \tag{12}\label{eq:first_law}
\end{align}
と，目指していた熱力学第一法則に辿り着きます．
　開いた系はモデルがかなり単純で，独立変数も\(t,\boldsymbol{x}\)から\(Q,p,V,U,T,S,H\)等になり，気象学者や熱の本質を知りたい人によっては扱いにくいモデル式となっており，どちらかと言うと工学的視点からエネルギーをどう取り出すか，気筒内の圧力や温度，体積等を変えることで観察しやすいようにできているのです．