速度\(v\)は単位時間に進む距離を意味するもので,単位を\( \rm{[m/s]}\)とするのはご存知かと思います.実は,単位を\( \rm{[m^3/(m^2\cdot s)]}\)と変形することができ,フラックス(流束)を表すこともできます.
フラックス(流束)とは?
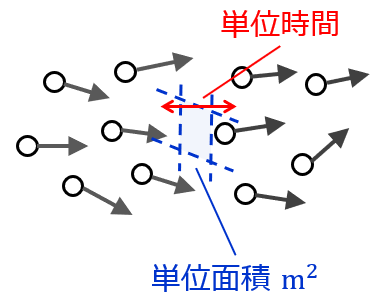
フラックス(流束)は,粒子と見たてられる物理量が,単位時間に単位面積を通過する量です.分母を\(\rm{[m^2\cdot s]}\)とした次元を持ちます.
例えば,電流や熱流束が挙げられます.電流は単位時間に導線の断面を通過する電荷の移動量です.\( I=en\bar{v} S\)という式を習いました.
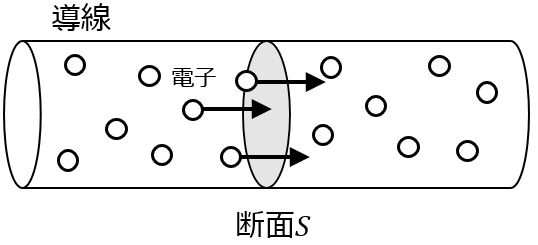
ただ,電流は断面積当たりの通過量で,単位も\(\rm[C/s]\)となっており,\(S\)を分母とした電流密度
\begin{align}
\boldsymbol{i} =en \boldsymbol{v}
\end{align}
が厳密にはフラック量になります.単位は \(\rm[C/(m^2\cdot s)]\)となります.
ちなみに\(S\)は基本的に形状に制限はないので,電流は真っ直ぐな導線の仮定から解放してあげて
\begin{align}
\boldsymbol{I} =\iint en \boldsymbol{v}\cdot \boldsymbol{S}
\end{align}
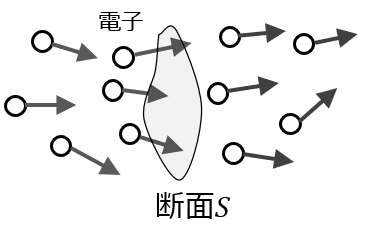
と積分形で書くことができ,電流が存在している空間上であれば,どんな方向を向いていても,計測面\(S\)がどのような形状でも表現できることができます.
熱流束も流束と名前が付いているだけあって,熱量のフラックス(流束)の意味します.熱量は単位が\(\rm{[J]}\)なので熱流束は\(\rm{[J/(m^2 \cdot s)]}\)となり
\begin{align}
q=\cfrac{d^2Q}{dS\,dt}
\end{align}
とかけます.
なお,磁束密度のように物理量の移動量を見立てる必要がない場合も,フラックスに含まれることがありますが,正確には流束密度というらしいです.ただ,流体力学では流束密度が出てくることはないと思いますので,気にしなくても大丈夫なはずです.
※見返してみるとこの式ちょっと気持ち悪いですね.熱流束については記事’熱伝導方程式‘の(b)に厳密に書いています.そのうち,本記事も修正できればと思っています.
体積フラックスと体積流量との関係
速度は\(\rm{[m^3/(m^2\cdot s)]}\)と書けるので,流体体積が通過するフラックス量を意味します.で,ここでは\(Q\)を流量とすると,流量の保存則は\(Q=vS\)と書けましたが,もう少し大人っぽく書くと速度を面積で積分した
\begin{align}
Q=\int \boldsymbol{v}(t, \boldsymbol{x})\cdot dS
\end{align}
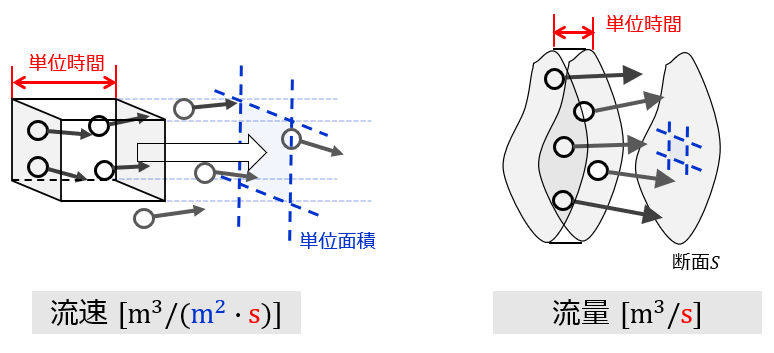
となります.
最後に,保存則は体積に対してより,質量や運動量に対して成り立つものなので,運動量の通貨量を取った
\begin{align}
Q=\int (\rho\boldsymbol{v})(t, \boldsymbol{x})\cdot dS
\end{align}
の方が汎用性が高くなり,圧縮性流体にも対応できます.
また,物理的意味が掴みやすいように「体積フラックス」なんて表現をしましたが「流束」の方が一般には伝わると思います。リュウソク…流速?…流束…


コメント