エントロピー

　エントロピーは下図(a)(b)(c)に示したように，空間，密度，温度の増加に伴って増加する量で，定義式は
\begin{align}
S(V,\rho,T)=k_B \,\rm log \it W \rm (\it V,\rho,T \rm) \tag{1}\label{eq:entropy}
\end{align}
と書けるそうです．世間では乱雑さとか何とか言いますが，そんな表現も数式も一旦忘れて，どんな風に増加するかシンプルに下図を見てみてください．

(a)体積の増加
　※系の体積が大きくなるとエントロピーが増加します．

(b)密度(粒子数)の増加

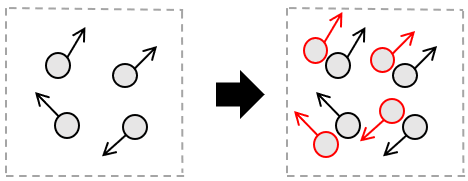
(c)温度の増加

　よくエントロピー増加で説明に用いられる例，2つ容器の間仕切りを外して閉じ込めた気体を混ぜ合わせるという話，これは(a)(b)を合わせたものとなっています．

　また，(c)のような温度とエンタルピーの増加増加関係は，熱力学でしばしば出てくるかと思います．
\begin{align} dS=\cfrac{dQ}{T} \tag{2}\label{eq:entropy-T}\end{align}
という式の方が馴染みがあるかもしれません．(c)は容器に囲まれた定積変化と見なした場合
\begin{align}
dQ&=dU \\
&=nC_V dT
\end{align}
が成立するため，
\begin{align}
\Delta S &=\int_{T_1}^{T_2}\cfrac{nC_V}{T}dt \\
&=n\rm C_V\log \biggl(\it \cfrac{T_2}{T_1} \rm\biggr)
\end{align}
と，式(\ref{eq:entropy})と同様に，対数で結んだ式の形になっていることが分かります．式(\ref{eq:entropy})と式(\ref{eq:entropy-T})は，ちゃんと繋がっているよと腑に落ちていただければ幸いです．

　式(\ref{eq:entropy})と別に
\begin{align}
dS=\cfrac{1}{T(Q)}dQ \tag{2}\label{eq:entropy-2}
\end{align}
と書くときがあります．私は
\begin{align}
\int_{S_1}^{S_2}dS=\int_{Q_1}^{Q_2}\cfrac{1}{T(Q)}dQ \tag{3}\label{eq:entropy-3}
\end{align}
と，書いた方が易しいじゃないかなって思っています．これが式(\ref{eq:entropy})と似ていることがさらっと見ていきましょう．

[1]定積変化
\begin{align}
\Delta Q&=\Delta U(p(T)) \\
&=mC_V\Delta T
\end{align}
が成り立つとして，
\begin{align}
\int_{S_1}^{S_2}dS&=\int_{T_1}^{T_2}\cfrac{1}{T}dQ(T) \\
&=\int_{T_1}^{T_2}\cfrac{1}{T}mC_V\,dT
=mC_V\left[\log T \right]_{T_1}^{T_2} \\
&=mC_V\log \cfrac{T_2}{T_1}
\biggl( =mC_V\log \cfrac{p_2(T_2)}{p_1(T_1)} \biggr)
\tag{4}\label{eq:const-vol}
\end{align}
と対数形の式になり，(c)の温度上昇の状態に当てはまります．

[2]定圧変化
\begin{align}
\Delta Q=mC_p\Delta T
\end{align}
が成り立つとして，
\begin{align}
\int_{S_1}^{S_2}dS&=\int_{T_1}^{T_2}\cfrac{1}{T}dQ(T)
=\int_{T_1}^{T_2}\cfrac{1}{T}mC_p\,dT \\
&=mC_p\log \cfrac{T_2}{T_1} \tag{5}\label{eq:const-ple} \\
&=mC_p\log \cfrac{V_2(T_2)}{V_1(T_1)}
\end{align}
と対数形の式になり，(a)の体積上昇と(c)の温度上昇の状態に当てはまります．

[3]定温変化
\begin{align}
\Delta Q=p\Delta V
\end{align}
が成り立つとして，
\begin{align}
\int_{S_1}^{S_2}dS&=\int_{V_1}^{V_2}\cfrac{1}{T(V)}dQ(V)
=\int_{V_1}^{V_2}\cfrac{1}{pV/nR}pdV \\
&=nR\log \cfrac{V_2}{V_1} \tag{6}\label{eq:const-tem}
\end{align}
と対数形の式になり，(a)の体積上昇の状態に当てはまります．

[4]断熱変化
　\(\Delta Q=0\)なので\(\Delta S=0\)です．