音は密度や圧力が振動して引き起こされます.このときの圧力を音圧と呼び,振動が伝わる速さを音速と言います.音圧はゲージ圧で表現することが多いようです.
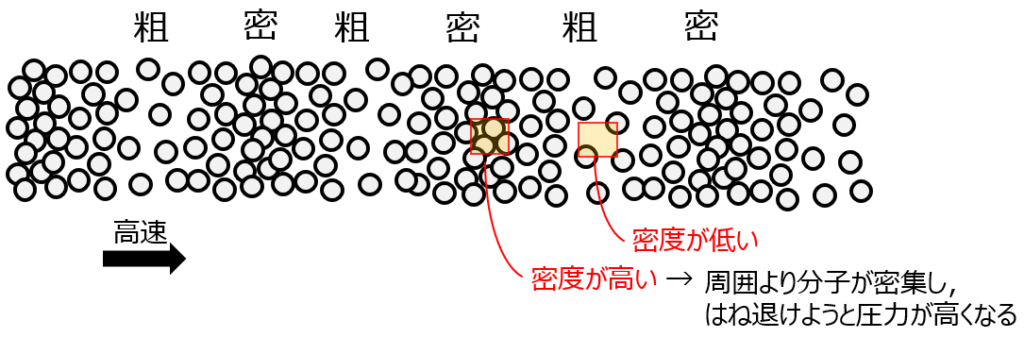
また,固体中でも液体中でも音の発生メカニズムは空気と同じで,密度や圧力の変化で起こります.固体や液体は,気体と違って分子が密になっているために音は速く伝わります.空気の音速は40m/s,水は1500m/s,氷は4000m/s程度です.
音は圧力/密度/温度等の熱的作用で変化を起こすものとし物性値として基本的に扱われます.ただ,風が吹いたりといった力学的作用により加減速したりもします.
音速と法則
音は媒質によらず次の(a)(b)(c)の性質が成り立ちます.
(a) 音速は圧力変化と密度変化の比を取った式
\begin{align}
c=\sqrt{\cfrac{\partial p}{\partial \rho}} \tag{1}\label{eq:soundSpeed}
\end{align}
に従います.弾性体の理論から導かれるみたいです.
(b) また,質量保存則\( \rho V=\rm{const} \)も成り立つため
\begin{align}
\rho\,\partial V+V\,\partial\rho=0 \tag{2}\label{eq:ConservationOfMass}
\end{align}
にも支配されます.
(c) 音は断熱的に圧縮されるので,熱力学第一法則
\begin{align}
0=\partial U+p\,\partial V \tag{3}\label{eq:FirstLowThermalDynamics}
\end{align}
も成り立ちます.
媒質を伝わる音は式 (\ref{eq:soundSpeed})(\ref{eq:ConservationOfMass})で支配されていますので,代入して解くと
\begin{align}
c=\sqrt{-\cfrac{V}{\rho}\biggl(\cfrac{\partial p}{\partial V}\biggr)}
\tag{4}\label{eq:soundSpeed2}
\end{align}
と書き直せます.ただ,\(\partial p/\partial V \)を解くことは難しく,音圧を求めるには液体/固体/気体でそれぞれ異なるアプローチが必要になってきます.
液体/固体/気体の場合
〈液体/固体の場合〉
まず,体積弾性率
\begin{align}
K=-V \biggl( \cfrac{\partial p}{\partial V} \biggr) \tag{5}\label{eq:BulkModulus}
\end{align}
を定義します.物体に圧力\(\partial p\)を加えたとき,体積変化\(\partial V\)が小さいほど\(K\)が大きくなるため,変形しにくさを示す量とされています.そして,式(\ref{eq:soundSpeed2})に(\ref{eq:BulkModulus})を代入して
\begin{align}
c=\sqrt{\cfrac{K}{\rho}} \tag{6}
\end{align}
と起き直すことで微分に依存しない音速の式が現れます.体積弾性率\(K\)は理科年表とか使って値を調べたり,弾性理論から割り出す方法等があります.
〈気体の場合〉
気体も体積弾性率を使った方法で音速を求めてもよいのですが,より厳密に断熱過程を利用した方法を用います.断熱のためポアソンの式
\begin{align}
pV^{\gamma}=\rm{const} \tag{7}
\end{align}
が成り立ち,対数をとって微分すれば
\begin{align}
\cfrac{\partial p}{P}+\gamma \cfrac{\partial V}{V} =0 \tag{8}
\end{align}
も同時に成り立ちます.ゆえに式に(2)に代入して整理すると
\begin{align}
c=\sqrt{\gamma\cfrac{p}{\rho}} \tag{9}
\end{align}
が成り立ちます.\(\gamma\)は比熱比を示します.


コメント