物理量の概観

　理論屋からすると，保存量やフラックスを中心とした物理的意味を持つ量と，計測量のカテゴリーに分けると物理学の世界が見渡しやすくなると思います．

　現象を読み解くには保存量やフラックス量が重宝されますが，それが測定できるかは話が別です．代表としてエネルギーで考えてみましょう．エネルギーは保存則ですが，例えば運動エネルギーの数量を割り出すのであれば，対象物の質量を計って，速度を計測して，\(\frac{1}{2}mv^2\)の式に乗せてといった過程を経ることになります．

　計測量は，さらに大きく二つに分けて考えます．一つは，長さ/時間/質量/温度の4指標で，それぞれ，定規/計り/時計/温度等，視覚的，感覚的または直接的に明瞭に測れる量です．これが基礎となって古典物理学が作られていることもあり，力学分野なんかを覗くと，大概この4つ単位の組み合わせで作られています．
　もう一つの測定量は，シンプルにこれまで述べてきた以外の量です．速度や圧力が代表格です．計測自体はできますが計測原理が複雑だったり，保存則のように強い法則性でないにも関わらず現象の考察に用いられたり，どっちつかずな顔を持った量です．

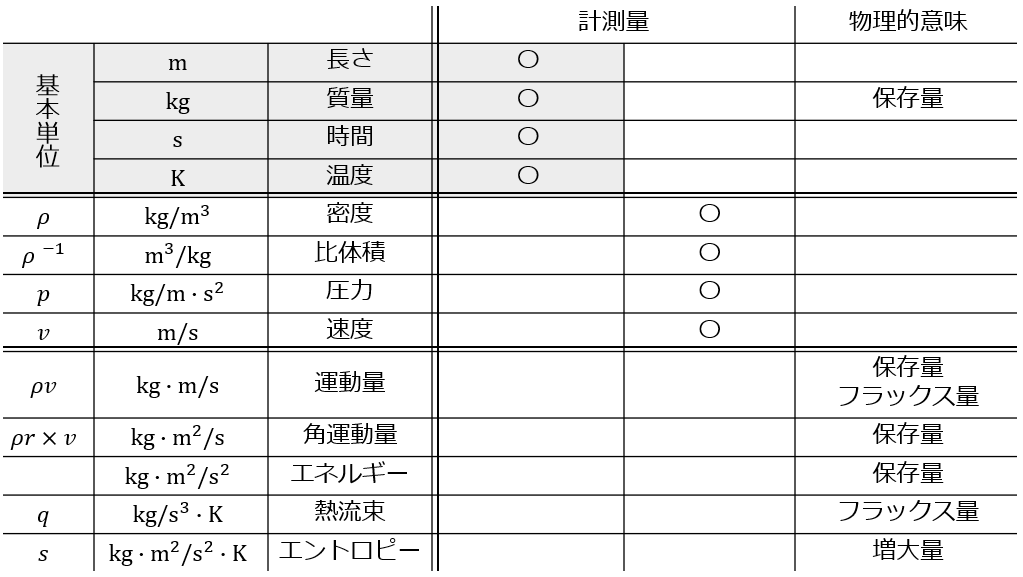
　実験時は計測量に，実験考察や数値実験では物理的に意味を持つ量に，重点を置く傾向があります．

　一方，これらとは別に，物理法則に当てはめることが難しい物性値が存在します．特に固体や液体であったり，温度変化によって変わりものが該当します．このような場合は，方程式を使うのではなく，理科年表にあるような予め調べられた関係を使用します．