温度の定義
温度は,誰もが日常的使っていることからも分かるよう冷温の程度を判断できる物理量で,計測によって定量判断できるよう提案されたものです.温度は,次の手順で定義します.
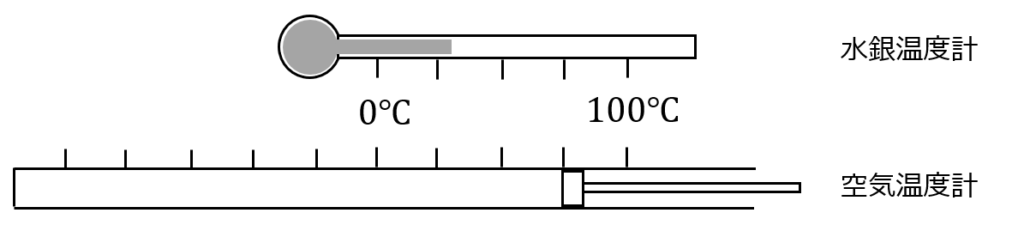
(1)常圧\(1.01325\times 10^5 \rm Pa\)の環境を確保し,水銀温度計を準備
(2)温度計を氷水につけ,水銀柱の伸び切ったところに印を付け\(0\)とする
(3)温度計を沸騰水につけ,水銀柱の伸び切ったところに印を付け\(100\)とする
(4)2つの印の間を\(100\)等分し,\(1\)目盛を\(1^\circ\rm C\)とする

次に,温度の下限値を調べます.水銀は\(-38.87^\circ\rm C\)で凝固するので,空気温度計に置き換えて調べます.
(5)空気温度計を準備
(6)空気温度計を水銀温度計の温度目盛りに合わせる
(8)\(0\,^\circ\rm C\)以下にも,例えば,\(-100^\circ\rm C\)目盛を伸ばす
(9)温度を下げることで空気を収縮させて,ピストンを下げていく
(10)ある程度温度を下げたら,ピストンがゼロになるところを予想する
ゼロになるところを温度下限とし,結果\(-273.15\,^\circ\rm C\)と分かります.なお,最低温度を\(0\)に設定したものがケルビン温度です.
次節で詳細を解説しますが,温度は分子の運動エネルギーを示すものです.どんな気体も温度を下げていくと液化・固化してしまいますが,いつまでも液化・固化しない永久気体が存在すると仮定した場合,\(-273.15\,^\circ\rm C\)では分子は運動を停止します.ここをゼロとしたケルビン温度という考え方がありますが,ゼロ状態から温度が上がるに従って分子の運動が激しくなっていきます.
温度計が目盛を決めるメカニズムは?
空気中の温度\(T\)に相当する熱エネルギーを持った気体が,温度計に次々にぶつかりガラス管の分子振動が激しくなり,その振動が更に水銀に伝わり,温度\(T\)相当の熱エネルギーを持つようになります.水銀の分子振動も激しくなって膨張したため,温度計の目盛りが表示されるといった順番になります.面白いのは,エネルギーが伝わって温度が定常状態になり,空気,ガラス管,水銀それぞれ同一温度になるのですが,1粒子単位のエネルギーは物質ごとに同じ量を持った状態になるのです.

温度の存在意義
個人的には,計測方法で目盛が本当に等分に割り当てられるのか厳密性に乏しさを感じる時があります.熱力学を探求していると存在意義に疑問を感じてしまうときもあります.ただ,存在するからには意味があります.なので,メリットを振り返ってみましょう.
メリット1:直接計測できる
熱力学では,エントロピーや内部エネルギー等沢山のキャラクターが現れますが,計測できないものばかりです.むしろ,計測して調べた温度から,それらを算出していく方が多いです.
メリット2:理解しやすい,一般人も共有しやすい
温度は天気予報でも当たり前のように毎日出ていて,体感的暑ければ高く寒ければ低いと,みんなが感覚的に共有している身近な物理量です.日常と物理学の架け橋になってくれるありがたい存在です.
メリット3:全てのものは同一温度になる
エアコンを\(25\,^\circ\rm C\)に設定した部屋があるとしましょう.理屈の上ではありますが,その部屋のソファーもコップの水もテーブルも,全てが\(25\,^\circ\rm C\)に向かって同一温度になります.熱力学は難しい学問ですが迷走したときに,意外に気持ちを落ち着かせてくれる魔法の性質だと思っています.
当たり前のことを振り返ることで,温度という物理量がツールとして使いやすくなってくれることを信じています.
温度は粒子の運動エネルギー
温度\(T\)とは1粒子の運動エネルギー\(m\bar{v}^2/2\)を示すものです.私のブログの展開では,これが温度や熱力学の出発点になりますので,
\begin{align}
T=\cfrac{2}{3k_{\rm{B}}} \biggl( \cfrac{1}{2}m\bar{v}^2 \biggr) \tag{1}\label{eq:T}
\end{align}

と,単位を\(\rm [J/K]\)とした温度と運動エネルギーを比例定数\(2/3k_{\rm{B}}\)をで結んだ式で表現できますと言って,話がこれで終わりにます.
ただ,感覚的に分かりやすいように,気体をモデルにした流体粒子を用いて,全ての粒子の速度が一様として説明をしてみます.一辺が\(L\)で囲まれた容器の中に,\(N\)個の気体粒子が存在し壁面に垂直に衝突する様子を思い浮かべましょう.一面のみへの衝突に注目しますので,対象となる粒子は\(N/6\)個です.また,実際の気体中では気体同士が衝突していますが,粒子が十分多いために壁と見立てることができます.そう仮定すると,ある気体粒子が壁から跳ね返ったときに衝突前の運動量\(m\bar{v}\)から衝突後の運動量\(-m\bar{v}\)に変換されるため,その差から\(2m\bar{v}\)の運動量を壁から受け取ったことが分かります.
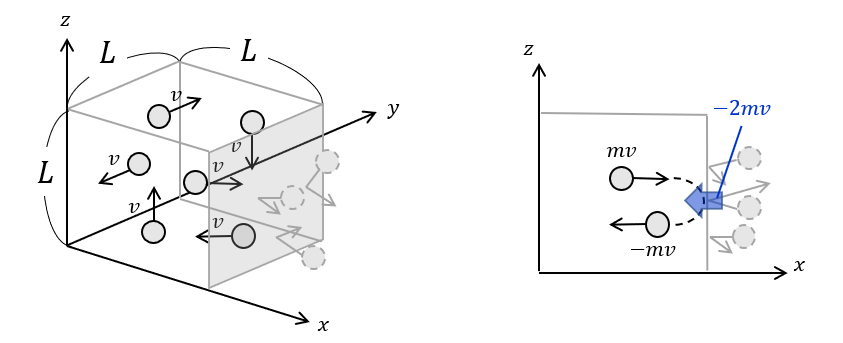
また,流体粒子は\(L/\bar{v} \, \rm [s]\)毎に対象の壁に衝突します.そのため,一回の衝突で粒子が壁にかける力を\(f\)とすると,力積の式から
\begin{align}
2m\bar{v}&=\int_{0}^{\frac{L}{\bar{v}}}f\,dt \\
&=f\int_{0}^{\frac{L}{\bar{v}}}dt
=f\cfrac{L}{\bar{v}}
\end{align}
となり,一個の粒子から受ける力は
\begin{align}
f=\cfrac{2m\bar{v}^2}{L}\tag{2}\label{eq:f}
\end{align}
となることが分かります.さて,実はこの壁面を押す力が圧力に相当します.1粒子だけだと非力ですが\(N\)個の粒子が容器の壁にぶつかることで圧力が形成されます.ただし,ここまで説明した仮定では壁面は6個存在し,この中の1個の壁の粒子の衝突に注目しているので,\(N/6\)の衝突によって圧力が形成されます.なので圧力は
\begin{align}
p&=\cfrac{\frac{N}{6}f}{L^2} \\
&=\cfrac{2N}{3L^3}\biggl( \frac{1}{2}m\bar{v}^2 \biggr).\tag{3}\label{eq:p}
\end{align}
と,粒子の運動エネルギーと圧力が結ばれることが分かります.ここからもっとイメージしやすいように,粒子を単原子分子の気体分子に置き換え,圧力を温度の式書き換えるため,式(\ref{eq:p})に気体の状態方程式を代入すると
\begin{align}
T&=\cfrac{2N}{3nR}\biggl( \frac{1}{2}m\bar{v}^2 \biggr). \tag{4}\label{eq:air-T4}
\end{align}
終わりに,アボガドロ数を\(N_A\)とすると\(N=n\times N_A\)であることから,
\begin{align}
T&=\biggl(\cfrac{2N_A}{3R}\biggr)\frac{1}{2}m\bar{v}^2 \tag{5}\label{eq:air-T5}
\end{align}
となって,温度は分子の運動エネルギーを示すことが分かます.
流体粒子の温度と運動量エネルギーの関係は,液体にだって分子振動があるので成り立ちます.気体で説明したのは,状態方程式というシンプル関係式があるために,前提条件も立てやすくて,式(\ref{eq:air-T5})まで簡単に導出できるためです.
また,温度と運動エネルギーの関係を結ぶ前に,圧力とも比例関係があると説明を挟みましたが,式(\ref{eq:p})からも読み取れるように,圧力の場合は粒子\(N\)にも依存して直接結ぶものではありません.この点は別途解説していきたいと思います.
内部エネルギー
分子運動エネルギーの閉じた空間での総量を内部エネルギーと呼びますが,この場合,粒子数は\(N\)と置かれるものの数えきれない数で,アボガドロ定数を使うのが一般的です.内部エネルギー\(U[\rm{J}]\)は式(\ref{eq:air-T4})より
\begin{align}
U&=N\biggl(\frac{1}{2}m\bar{v}^2\biggr) \\
&=\cfrac{3}{2}nRT \tag{6}\label{eq:inter-ene-U1}
\end{align}
と書けます.
開いた系の場合,単位体積に注目しますので,内部エネルギー\(u\)の単位は\([\rm{J/m^3}]\)となります.適当に選んだ空間体積\(V\)に含まれる粒子数を\(N_V\)とし
\begin{align}
u&=\cfrac{N_V\biggl(\frac{1}{2}m\bar{v}^2\biggr)}{V}, \tag{8}\label{eq:inter-ene-u}
\end{align}
質量密度を\(\rho\)とすると
\begin{align}
\rho=\cfrac{N_V\, m}{V} \tag{9}\label{eq:mass-density}
\end{align}
と書けます.式(\ref{eq:inter-ene-u})に(\ref{eq:mass-density})を代入して
\begin{align}
u&=\frac{1}{2}\rho\bar{v}^2 \tag{10}\label{eq:mass-density-U2}
\end{align}
となります.
1粒子の運動エネルギー
まず,式(\ref{eq:T})の関係について,ボルツマン定数\(k_{\rm{B}}\)という係数が出てきた理由からです.式(\ref{eq:T})を変形すると
\begin{align}
\cfrac{1}{2} m\bar{v}^2
=\cfrac{3}{2}k_{\rm{B}}T \tag{1′ }\label{eq:particle-ene}
\end{align}
となります.式(\ref{eq:inter-ene-U1})と比較すると,式(\ref{eq:particle-ene})は1粒子あたりのエネルギー,式(\ref{eq:inter-ene-U1})は\(N\)個の粒子のエネルギーであることが分かるでしょう.

次に,式(\ref{eq:particle-ene})に「\(3\)」という気持ち悪く見える数字が入っている理由についてです.導入した平均速度は存在する全ての粒子の平均を取ったもので
\begin{align}
\bar{v}=
\sqrt{{\overline{v_x}}^2+{\overline{v_y}}^2+{\overline{v_z}}^2}
\end{align}
と書けますが,空間3成分に対しても平均的な\(\overline{v_x}=\overline{v_y}=\overline{v_z}\)の関係でもありますので
\begin{align}
\bar{v}=3\overline{v_x}
\end{align}
となります.式(\ref{eq:inter-ene-U1})は
\begin{align}
\cfrac{1}{2} m{\overline{v_x}}^2
=\cfrac{1}{2}k_{\rm{B}}T \tag{11}\label{eq:particle-ene-x}
\end{align}
となり「3」が消えました.式(\ref{eq:mass-density-U2})は\(\bar{v}\)を注目した運動論的に,式(\ref{eq:particle-ene-x})は\(T\)に注目した熱力学的に有効なものと見るとよいでしょう.そう,式(\ref{eq:particle-ene-x})は次節で説明する”エネルギー等分配の法則”で絶大な力を発揮します.
エネルギー等分配の法則
気体の形や力,速度は,真ん丸と仮定し,特に速度に着目してきましたが3方向に分けられるとしました.これは単原子分子の場合に成り立ちます.2原子分子になりますと,棒の状態で動いてると考え回転が発生し,回転運動成分が3方向の直線運動に加え,2つ必要になります.また,さらに2原子分子でも,原子間で振動が生じもう1成分加える必要が出てきます.
このように動き回りに必要な成分数に分けられ,それらを自由度\(f\)と呼びます.自由度はこんな感じで分子の種類で異なり,単原子分子では\(\frac{3}{2}k_{\rm{B}}T\)のエネルギーを持っていて,これを3つの成分ごとに,それぞれが\(\frac{1}{2}k_{\rm{B}}T\)のエネルギーを持っいます.振動する2原子分子に拡張して考えた場合も,2つの回転成分と1つの振動成分も同じ量の\(\frac{1}{2}k_{\rm{B}}T\)だけ割り当てられます.このように自然界では同じ量だけエネルギーを割り振られるため,エネルギー等分配の法則と呼ばれます.絶対的な法則の一つで,これについては何故?を追求せず,こういうものだとまず納得してみてください.

熱の状態を温度\(T\)を基準にしたとき,気体の種類によって蓄えている内部エネルギーは等温度領域で,それぞれ持っている内部エネルギーは異なります.内部エネルギーを比較したいときに必要な見方です. 一方,物理的な考察をするとき,内部エネルギーを同一に見る方法があります.例えば,定量の内部エネルギーを与えた時に気体が変化する温度を考えたいときはこっちが向いています.
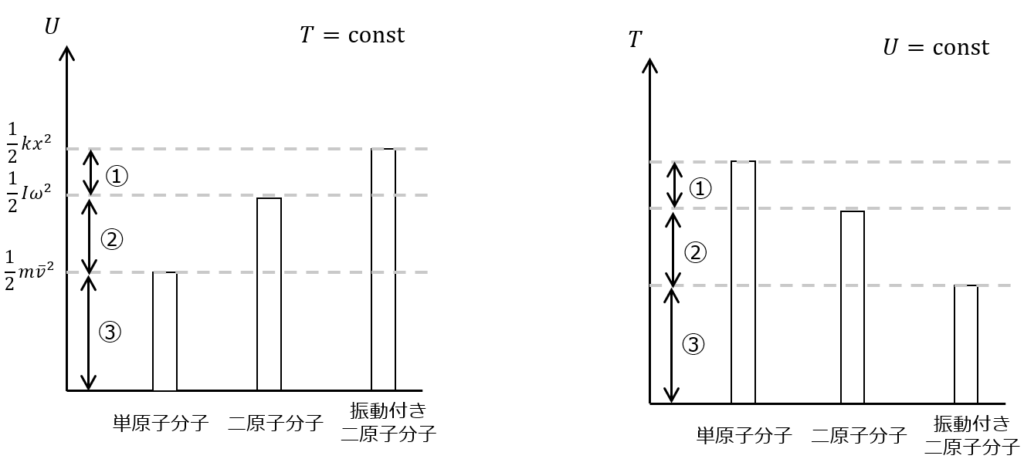
固体,液体,気体の内部エネルギーと温度
水銀温度計で,空気(気体)とガラス(固体),水銀(液体)がそれぞれ同じ温度になると説明しましたが,サクッと内部エネルギーが異なる理由も考えてみましょう.気体は分子が運動していて直線運動や回転運動をしていると説明しましたが,固体は分子間で結合され,その間でバネのように伸び縮みが起こるようなもので,熱が入るとバネが膨張し,延びたり振動が激しくなったりします.液体は,気体のように運動する性質と,固体のバネのように緩く結合している性質を持っています.値の大小を付けるのは難しいですが,全く状態が異なることから内部エネルギーもそれぞれであることは察しが付くでしょう.



コメント