エンタルピーを復習

　エンタルピーは物理の書籍を読んでいてもあまり姿を現さず。出てきたとしても「\( H=U+pV \)と定義する」と急に現れ、それ以上に深い説明もなく..．と言いうのも、エンタルピーは単純明快にエネルギーの総量であって、それに尽きるから説明するまでもないのです。

　熱力学では、内部エネルギー\(U\)やらエントロピー\(S\)やら不可解な登場人物が沢山いて、その中にエンタルピーとい奇妙な名前の見せかけ異星人が出てくるから困ってしまうのです。 今回は、皆が敢えて説明しないエンタルピーを、下手くそなりに咀嚼してみたいと思います。

　 熱量\(Q\) は物体の中を入ったり出たりする熱のエネルギー量のことで、温度\(t_1\)の水に\(t_2\)になるまで熱量\(Q\)を与えた場合
\begin{eqnarray}
Q=mc( t_2 – t_1 ) \tag{1}\label{eq:heatValue}
\end{eqnarray}
なんて書き方がされたり、または
\begin{eqnarray}
\Delta Q= \Delta U + p\Delta V \tag{2}\label{eq:heatValue-eq}
\end{eqnarray}
と書いたりしますよね。で、なぜか式(\ref{eq:heatValue-eq})が現れた流れで、しれっとエンタルピー
\begin{eqnarray}
H=U+pV \tag{3}\label{eq:enthalpy}
\end{eqnarray}
が説明もなく登場したりしますよね。\(Q=U+pV\)と書いてもよい気もしますが…
ただ、以下2つの説明する点で、\(Q\)と \(H\)は別ものとして扱うようです。

(1) \(Q\)は熱的なエネルギーだけ扱うのに対し、\(H\)は力学的エネルギーも含めた量である
(2) \(Q\)と違い\(H\)は明確な基準値がある

それでは、(1)(2)についてもう少し嚙み砕いていきましょう。

　式(\ref{eq:enthalpy})を\(\Delta\)だけ動かすと

\begin{align}
\Delta H &=\Delta U+\Delta(pV) \\
&=\Delta U + p\Delta V +V\Delta p \tag{4}\label{eq:Delta-enthalpy}
\end{align}
となります。式(\ref{eq:heatValue-eq})に\( V\Delta p \)が加わった形をしてますが、これは力学的なエネルギーとして現われる項っぽいです。 \( V\Delta p \) はどんな物理的性質を持ったものなのか、以下例をご紹介します。

＜ベルヌーイの定理の場合＞

　\(H\)はエネルギーの総量と説明しましたように、式(\ref{eq:Delta-enthalpy})のエネルギー量を持つ物体が速度\(v\)で運動していたとき
\begin{align}
\Delta H = \Delta \biggl(\frac{1}{2}mv^2 \biggr) +\Delta U + p\Delta V +V\Delta p \tag{5}\label{eq:Delta-enthalpy+v}
\end{align}
と、運動エネルギーを加えることができます。さてさて、ここから更に熱的変化を外してみますと、\(\Delta U=0,\,\, p\Delta V=0\)として
\begin{align}
\Delta H = \Delta \biggl(\frac{1}{2}mv^2 \biggr)+V\Delta p \tag{6}\label{eq:Delta-enthalpy+Bern}
\end{align}
となります。特に\(\Delta H =0\)のエネルギーが保存された状態の時って、運動エネルギーが増減した場合、圧力がその分減ったり増えたりします。これって、ベルヌーイの定理であること分かりますかね？以前、運動エネルギーが静圧に変化することを説明したことがあります。エンタルピーは熱力学的エネルギーに加えて、力学的エネルギーの変化よって生じる圧力変化も同時に含めて確認することができます。

　\(Q\)は熱移動量であって、 式(\ref{eq:heatValue})では温度差を取っていることから、 式(\ref{eq:heatValue-eq}) では\(\Delta Q\)と変化を与えていることからも分かると思います。だから、下図のように \(Q\) はエネルギーの基準点から表した量ではありません。

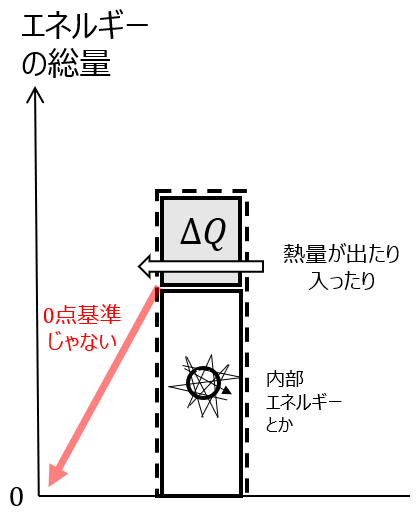
　 一方、\(H\)はエネルギーの総量なので、絶対温度\(0\)が基準点となり、下図のように物体のエネルギーを\(0\)点から、それぞれのエネルギー加えていったものになってます。

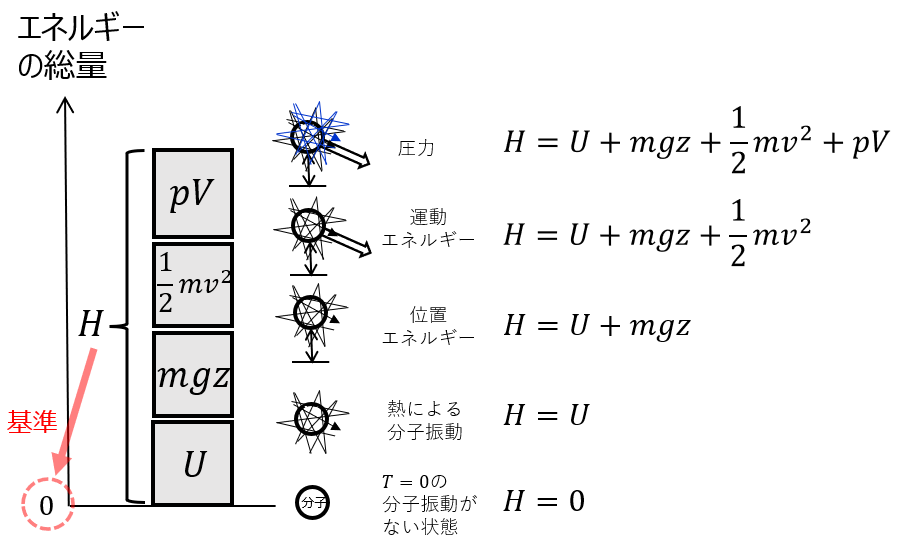
　実際のところ、\(U\)が増加すると\(p\)や\(V\)も増加し分けて書くことはできませんし、\(H=0\)の常態なども物理的にあり得るものではありません。エンタルピーについて詳しい説明を放棄する理由はここにもあるのかもしれません。

　熱力学ではピストンの中で一様状態になったものを考察していると思いますが、流体力学である点\( \boldsymbol{x} \)におけるエンタルピーを知りたいので、単位体積当たりに換算すると便利になります。なので、\(h=H/V,u=U/V,\rho=m/V\)とおいて
\begin{align}
h = u + \rho g z +\frac{1}{2}\rho v^2+ p \tag{7} \label{eq:enthalpy-vol}
\end{align}
とかけます。また、単位質量当たりだと \(h^{\prime}=h/\rho,u ^{\prime}=u/\rho\)とおいて
\begin{align}
h ^{\prime} = u^{\prime} + g z +\frac{1}{2}v^2+ \frac{p}{\rho} \tag{8} \label{eq:enthalpy-mass}
\end{align}
とかけます。 \(h^{\prime} \)を比エンタルピーと呼ぶこともあります。