移流項の物理的な意味について,直感的に捉えられるか考えてみたいと思います.ナビエ-ストークス方程式の時間項と移流項だけを残した
\begin{align}
\cfrac{\partial u_i}{\partial t}=-u_k \cfrac{\partial u_i}{\partial x_k}, \qquad i=1,2,3,
\end{align}
の式から,移流項によってどのように加速するか知るにあたり,更に2次元化した\(x\)成分
\begin{align}
\cfrac{\partial u(x,y,t)}{\partial t}=-u\cfrac{\partial u}{\partial x} -v\cfrac{\partial u}{\partial y}
\end{align}
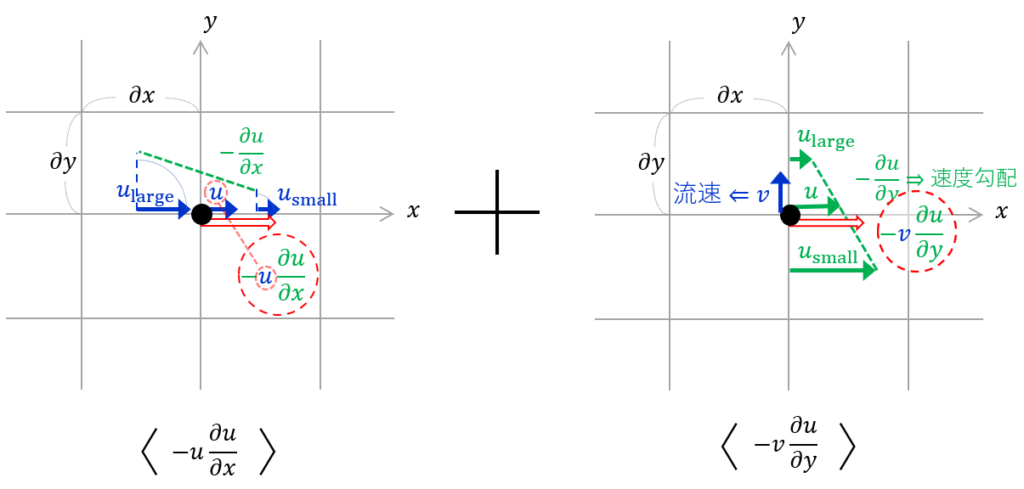
を準備します.次に,下図のような微小なグリットで構成された空間図を用意してみました.特に右側の\(-v\frac{\partial u}{\partial y}\)の項に注目してみます.するとどうでしょう.速度勾配 \(-\frac{\partial u}{\partial y}\) があると,流速\(v\)に乗せられて,速度勾配が平滑化される方向に向かい,\(u\)が運ばれた分だけ\(x\)方向の加速度に変わります.もちろん,流速\(v\)が速度勾配\(-\frac{\partial u}{\partial y}\)に対し小さい方から大きい方に向いていれば,速度勾配は更に大きくなり,移流項の加速度は反対方向に発展します.
また,運動量で考えた式
\begin{align}
\cfrac{\partial(\rho u_i)}{\partial t}=-u_k \cfrac{\partial (\rho u_i u_k)}{\partial x_k}, \qquad i=1,2,3,
\end{align}
では,\(x\)成分については
\begin{align}
\cfrac{\partial u(x,y,t)}{\partial t}=-\cfrac{\partial \{u(\rho u)\}}{\partial x}-\cfrac{\partial \{v(\rho u)\}}{\partial y}
\end{align}
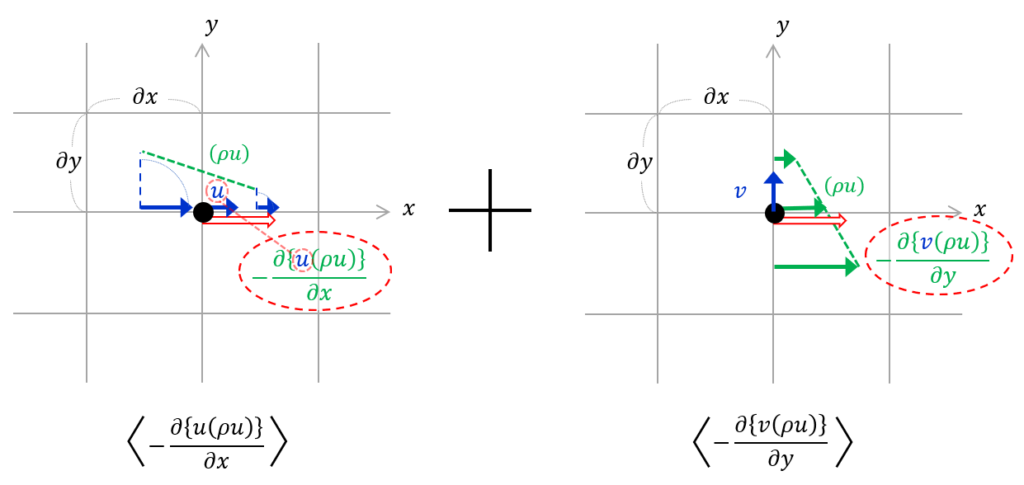
とも書けて,特に\(-\frac{\partial \{v(\rho u)\}}{\partial y}\)に注目してみると,運動量 \((\rho u)\) に流速\(v\)を乗じた状態に対し,勾配を取ったものが移流項となることが分かるかと思います.図とは若干相容れない部分はありますが,いずれにしても,速度\(v\)が運動量 \((\rho u)\) の勾配を埋めるように働き,その時に加速度 \(-\frac{\partial \{v(\rho u)\}}{\partial y}\) が発生するメカニズムになっていると考えられます.


コメント