ナビエストークス方程式の最終項,粘性項について考えいきましょう.
\begin{align}
\nabla(\lambda\nabla(\rho\boldsymbol{u}))
\end{align}
と,こんな感じに書く式についてですね.今回は式の説明はしませんが,どんな風に現象を捉えるのか考えてみましょう.粘性項は拡散項と呼ばれたり摩擦項と呼ばれたりもします.まず,それぞれの意味を確認からです.
粘性…字の如くネバネバの度合いのことで,流体が運動しているときの物性は
動粘性と呼ばれます.
拡散…粒子そのものや熱,運動量等が散らばりながら広がる物理現象です.
固体内の熱広がりであったり,2種の気体が混ざって均一になる様子だったり,
流体力学の世界に踏み入らなくても伝熱学や化学等で見かけたりします.
摩擦…固体同士のこすれで熱が発生しますが,流体固体同士,流体流体同士つまり流体内でも,
運動エネルギーは熱や音に変わっていきます.
なんだか,意味が同じような違うようなな感じですよね.では,どんな物理現象が起きているか見てながら考えていきましょう.
粘性,拡散,摩擦の関係
流体は大きい渦や小さい渦がひしめき合って存在します.渦が隣接する渦に物理量を渡し,渡され,段々とその物理量が空間的になだらかになっていき広がっていきます.なだらかになることから”粘性”,広がることから”拡散”と呼ばれことは想像に容易いでしょう.

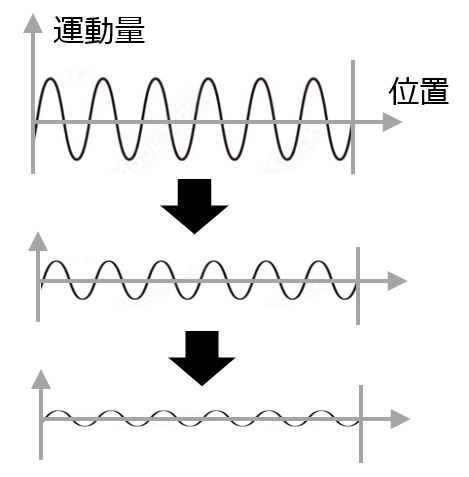
渦はまた,下図に示したように,矢印のぶつかり合う方向に流れができやすいため,結果”摩擦”が生じ,運動エネルギーが消滅し熱エネルギーに変化されます.なので,バケツに入った水を延々とかき混ぜ続けるなんてことをすると温度が上がってくるのです.

一旦話をここでまとめますと,拡散は物理量を運び広げ一様にする現象で,摩擦はずり方向に発生する運動量をゼロに持っていく力です.また,粘性は流体力学を中心に出てくる用語ですが,拡散と摩擦は物理学全般で出てきます.私が思うに粘性は渦運動が引き起こす現象の総称と解釈していて,拡散と摩擦の両方を含んだものと捉えています.ただ再三言いますが,これらの用語に厳密な使い分けはあまりされいないので意味の追求には神経質にならないでください.
拡散について補足
ただ,拡散について勘違いしてほしくないことは,流体運動をゼロにするのではなく,なだらかにするだけのものです.例えば,下図のように左側だけ移動する壁だった場合,波打ちは消えますが,移動壁に引きずられて運動量は存在し続けます.
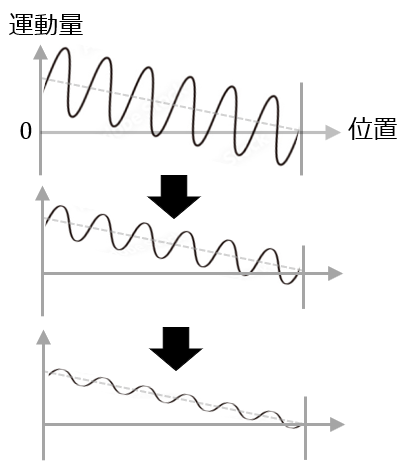
摩擦について補足
摩擦によるエネルギー消失は微々たるもので,これが数値計算モデルに組み込まれたり,考察対象として扱われることはまずありません.壁面上については,流体内部と同様に流動により熱は生じますが,仮定上,壁から運動量ゼロを受け取るとします.

因みに摩擦が拡散を凌駕し大きく寄与するとしたら,摩擦は運動量をゼロにする性質がありますので,波打ち現象をある程度残しながら運動量ゼロに近づく分布をきっと見せるのでしょう(移流項の存在しないと仮定して).

分子粘性と乱流粘性
粘性は分子粘性と乱流粘性に分けられます.対流として発生する渦が乱流粘性で,小さい渦の集まりとして形成されていて,さらにこの小さい渦はより小さい渦の集まりで形成され,延々同構造が繰り返されます.しかし,微小の現象を考えてみると,分子同士が分子運動で物理量を交換し拡散現象が発生します.これが分子粘性ですが,乱流渦をどんどん小さいサイズに視点を切り替えていくと,あるところから分子粘性が卓越し支配状態になります.このとき,流れは層流状態になります.



コメント