高校では運動方程式を
\begin{align}
m\cfrac{d\boldsymbol{u}}{dt}=\boldsymbol{F} \tag{1}\label{eq:mot-eq}
\end{align}
と学んだと思います。ニュートンの第二法則とも呼ばれ、物理学を語る上で最も重要な式であり、運動方程式といえば式(\ref{eq:mot-eq})で刻み込まれちゃっています。でもでも、流体力学を修得するなら
\begin{align}
\cfrac{d(m\boldsymbol{u})}{dt}=\boldsymbol{F}
\quad\biggl(または\cfrac{dp}{dt}=\boldsymbol{F}だったり\biggr) \tag{2}\label{eq:NEWmot-eq}
\end{align}
とアップデートしてください!!そして、流体力学は運動量を中に心出来上がっていることを意識してもらい、ナビエ-ストークス方程式の大元の式である
\begin{align}
\cfrac{d}{dt}\int_V(m\boldsymbol{u})dV
=\boldsymbol{F}_{\text{表面力}}+\boldsymbol{F}_{\text{体積力}} \tag{3}\label{eq:NSmot-eq}
\end{align}
がキーになってることを理解していただければ幸いです。
本題
まず、流体は体積が縮んだり膨張したりする圧縮性があることを思い出してください。なので、流体の質量は変化するので質点\(m=\rm{const}\)ではなく、時間\(t\)を変数とした\(m(t)\)と書きます。ちなみに、本件ではラグランジュの視点で展開していくので、位置\(\boldsymbol{x}\)も\(t\)の従属の変数となり\(m(\boldsymbol{x}(t))\)とも書けます。さて、式(\ref{eq:NEWmot-eq})に変数を入れてみると
\begin{align}
\cfrac{d}{dt}\Bigl( m(\boldsymbol{x}(t))\,\boldsymbol{u}(\boldsymbol{x}(t)) \Bigr)=\boldsymbol{F}
\tag{4}\label{eq:NEWmot-eq+}
\end{align}
となります。質点系の問題は\(m=\rm{const}\)の場合なので、式(\ref{eq:NEWmot-eq})は式(\ref{eq:mot-eq})を含んでおり、力学で扱う問題は質点系に帰着してしまうものばかりなので、どうして式(\ref{eq:mot-eq})は影が薄くなってしまいます。
さて、ここから更に式(\ref{eq:NEWmot-eq+})を発展させていきましょう。式(\ref{eq:NEWmot-eq+})では位置の変数は\(\boldsymbol{x}\)の一点になっていますが、流体は複数の点の集合で見立てます。流体内部各々の箇所では質量密度が異なりますので、下図のように各々の点\(\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots\)に運動量を与える必要があります。
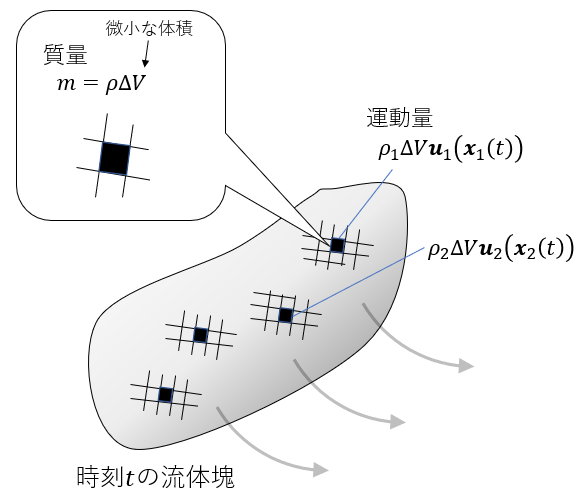
図のように、ある一部の流体領域を切り取った流体塊の運動量を考えてみると
\begin{align}
m\boldsymbol{u} &= \lim_{\Delta V \to 0}
\bigl\{
\rho_1 \Delta V\boldsymbol{u}_1(\boldsymbol{x}_1(t))+
\rho_2 \Delta V\boldsymbol{u}_2(\boldsymbol{x}_2(t))+ \cdots
\bigr\} \\
&=\lim_{\Delta V \to 0} \sum_{i=1}^{\infty} \rho_i \boldsymbol{u}_i(\boldsymbol{x}_i(t))\Delta V \\
&= \int_V \rho \boldsymbol{u}(\boldsymbol{x}(t)) dV \tag{5}\label{eq:Momentum}
\end{align}
と書けます(ちょっと強引な式展開ですが…)。よって、流体を考えるときは式(\ref{eq:NEWmot-eq+})(\ref{eq:Momentum})より
\begin{align}
\cfrac{d}{dt}
\int_V \rho \boldsymbol{u}(\boldsymbol{x}(t)) dV=\boldsymbol{F}(t)
\tag{6}\label{eq:NEWNSmot-eq}
\end{align}
が流体塊の運動方程式になります。流体力学の多くの書籍では更にここから一歩踏み込んで、\(\boldsymbol{F}(t)\)に表面力である圧力や、体積力である重力を当てはめて式(\ref{eq:NEWNSmot-eq})を
\begin{align}
\cfrac{d}{dt}
\int_V \rho \boldsymbol{u}(\boldsymbol{x}(t)) dV
=\int_S \boldsymbol{p}\, dS + \int_V \rho\boldsymbol{g}\, dV
\tag{7}\label{eq:NEWNSmot-eq+}
\end{align}
なんて形で書かれているかと思います。これが、式(\ref{eq:NSmot-eq})のことです。
ナビエ-ストークス方程式は
\begin{align}\cfrac{\partial u}{\partial t} +\cdots\end{align}
をよく見かけますが、圧縮性流体はもちろん乱流でも運動量を重視した
\begin{align}\cfrac{\partial (\rho u)}{\partial t} +\cdots\end{align}
が出てきますので心に留めておいてください。
保存則について(おまけ)
ついでの説明をすると、上図の流体塊は保存則なら基本的に何でも満たしてくれます。だから
\begin{align}
&\int_V \rho dV = \rm{const}, \quad (\text{質量保存則})\\
&\int_V (\rho\boldsymbol{u}) dV = \rm{const}, \quad (\text{運動量保存則}) \\
&\int_V \biggl(\frac{1}{2}\rho\boldsymbol{u}^2 \biggr) dV = \rm{const} \quad (\text{エネルギー保存則})
\end{align}
と書くことができます。流体力学では上式をまとめて三つの保存と呼んでいて、これらが成り立つことを前提に話が進んでいきます。
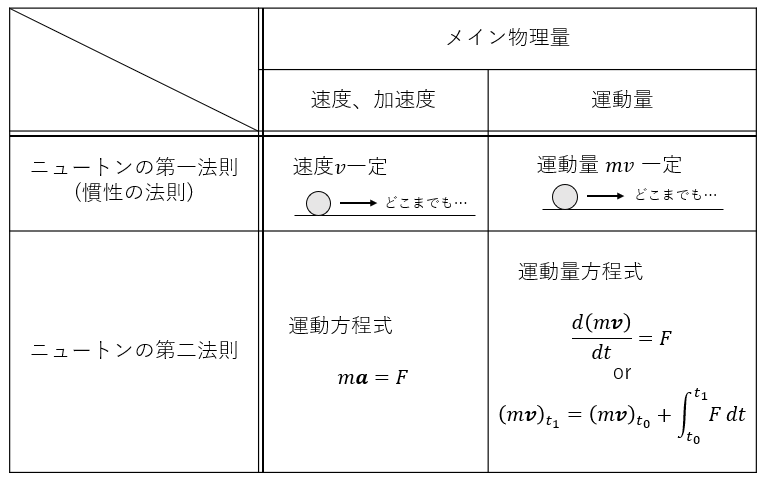
また、運動方程式を勉強していると、加速度や力が主役のように見えますが、視点を保存則である運動量に目を向けると、力は運動量を時間変化させる脇役のようにも言えて、私はこちらの方が本質的だと思っています。ニュートンの法則を運動方程式に置き換えてみました。
せっかくなので、速度\(v_0\)で転がってた物体が坂道を下ったあと、速度はどのようになるのか、運動量方程式で考えてみました。
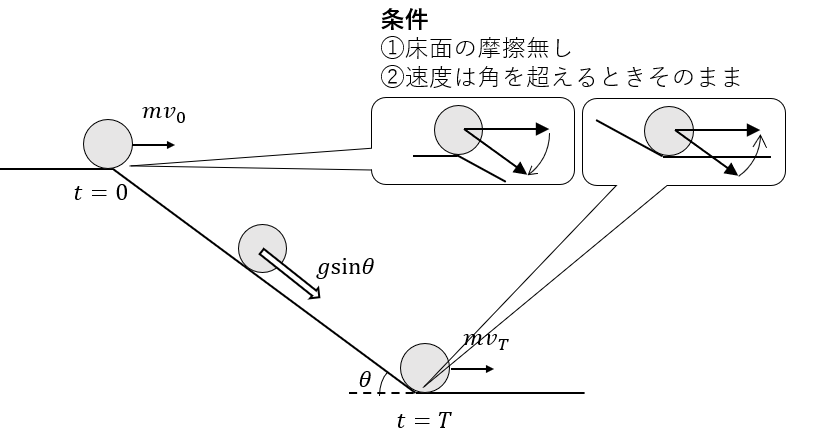
\begin{align}
mv_{T} &=mv_{0}+\int_{0}^{T}mg\sin\theta dt \\
&=mv_{0}+mg\sin\theta\bigl[\, t \,\bigr]_{0}^{T} \\
&=mv_{0}+mgT\sin\theta,
\end{align}
よって
\begin{align}
v_T=v_0+gT\sin\theta.
\end{align}
確かに、速度は高校生の時に習った\(v=v_0+at\)の形になりました。わざわざ,坂を下りる時間\(T\)を与える点が滑稽で実用性に欠けていますが,運動量に注目して運動の様子を解くことも可能なようです。


コメント